6.4 Práctica en R
Para este ejemplo cargamos la librería ISLR y utilizamos el conjunto de datos de Smarket.
Veamos información sobre los datos Smarket
?Smarket## starting httpd help server ... donehead(Smarket)## Year Lag1 Lag2 Lag3 Lag4 Lag5 Volume Today Direction
## 1 2001 0.381 -0.192 -2.624 -1.055 5.010 1.1913 0.959 Up
## 2 2001 0.959 0.381 -0.192 -2.624 -1.055 1.2965 1.032 Up
## 3 2001 1.032 0.959 0.381 -0.192 -2.624 1.4112 -0.623 Down
## 4 2001 -0.623 1.032 0.959 0.381 -0.192 1.2760 0.614 Up
## 5 2001 0.614 -0.623 1.032 0.959 0.381 1.2057 0.213 Up
## 6 2001 0.213 0.614 -0.623 1.032 0.959 1.3491 1.392 Upsummary(Smarket)## Year Lag1 Lag2
## Min. :2001 Min. :-4.922000 Min. :-4.922000
## 1st Qu.:2002 1st Qu.:-0.639500 1st Qu.:-0.639500
## Median :2003 Median : 0.039000 Median : 0.039000
## Mean :2003 Mean : 0.003834 Mean : 0.003919
## 3rd Qu.:2004 3rd Qu.: 0.596750 3rd Qu.: 0.596750
## Max. :2005 Max. : 5.733000 Max. : 5.733000
## Lag3 Lag4 Lag5
## Min. :-4.922000 Min. :-4.922000 Min. :-4.92200
## 1st Qu.:-0.640000 1st Qu.:-0.640000 1st Qu.:-0.64000
## Median : 0.038500 Median : 0.038500 Median : 0.03850
## Mean : 0.001716 Mean : 0.001636 Mean : 0.00561
## 3rd Qu.: 0.596750 3rd Qu.: 0.596750 3rd Qu.: 0.59700
## Max. : 5.733000 Max. : 5.733000 Max. : 5.73300
## Volume Today Direction
## Min. :0.3561 Min. :-4.922000 Down:602
## 1st Qu.:1.2574 1st Qu.:-0.639500 Up :648
## Median :1.4229 Median : 0.038500
## Mean :1.4783 Mean : 0.003138
## 3rd Qu.:1.6417 3rd Qu.: 0.596750
## Max. :3.1525 Max. : 5.733000En este caso la variable Y que queremos predecir/explicar es la variable Direction, y las variables independientes son Lag1, Lag2, Lag3, Lag4, Lag5 y Volume.
Veamos que valores toma la variable Direction
levels(Smarket$Direction)## [1] "Down" "Up"Vemos que es una variable binaria que toma valores Downo Up.
Antes de continuar pasamos esos valores a 0 o 1, respectivamente.
Smarket$Direction <- ifelse(Smarket$Direction == 'Up', 1, 0)Para realizar la regresión logística en R utilizaremos la función glm.
Se puede observar en el código siguiente, que como nuestro Target es binario, el parámetro family lo debemos fijar a binomial.
reg_logis <- glm(Direction~Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + Volume,
data = Smarket,
family = binomial)Veamos que hemos obtenido
summary(reg_logis)##
## Call:
## glm(formula = Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 +
## Volume, family = binomial, data = Smarket)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.446 -1.203 1.065 1.145 1.326
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.126000 0.240736 -0.523 0.601
## Lag1 -0.073074 0.050167 -1.457 0.145
## Lag2 -0.042301 0.050086 -0.845 0.398
## Lag3 0.011085 0.049939 0.222 0.824
## Lag4 0.009359 0.049974 0.187 0.851
## Lag5 0.010313 0.049511 0.208 0.835
## Volume 0.135441 0.158360 0.855 0.392
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1731.2 on 1249 degrees of freedom
## Residual deviance: 1727.6 on 1243 degrees of freedom
## AIC: 1741.6
##
## Number of Fisher Scoring iterations: 3Los coeficientes de la regresión logística obtenida serán:
coef(reg_logis)## (Intercept) Lag1 Lag2 Lag3 Lag4
## -0.126000257 -0.073073746 -0.042301344 0.011085108 0.009358938
## Lag5 Volume
## 0.010313068 0.135440659Como se hace en los otros modelos, la función predict la utilizaremos para predecir un nuevo conjunto de datos a partir de nuestro modelo de regresión logística ajustado.
Para un modelo binomial predeterminado, las predicciones serán de log-odds (probabilidades en la escala logit). Como vemos en el código a continuación, utilizamos el argumento type = response para guardar la predicción de las probabilidades.
glm.probs <- predict(reg_logis,
type = "response")Lo que hacemos a continuación es dar a una observación el valor del target \(1\) o \(0\) en función a la probabilidad obtenida. El corte en la probabilidad en este caso lo ponemos en \(0.5\), es decir, si la predicción que se ha obtenido de la probabilidad es menor que 0.5, le damos el valor \(0\), y sino el valor \(1\). El código que hace esto es de la siguiente manera:
glm.pred <- rep(1, nrow(Smarket))
glm.pred[glm.probs < .5] <- 0Ahora, obtenemos la matriz de confusión, en el que podemos comparar el valor de la predicción obtenida (filas) con el verdadero valor (columnas). De esta manera, lo que está en la diagonal principal será lo que se ha predecido correctamente.
table(glm.pred, Smarket$Direction) ##
## glm.pred 0 1
## 0 145 141
## 1 457 507observamos la media de los valores que se ha predecido bien:
mean(glm.pred == Smarket$Direction)## [1] 0.5216y la media de los que se han predecido mal:
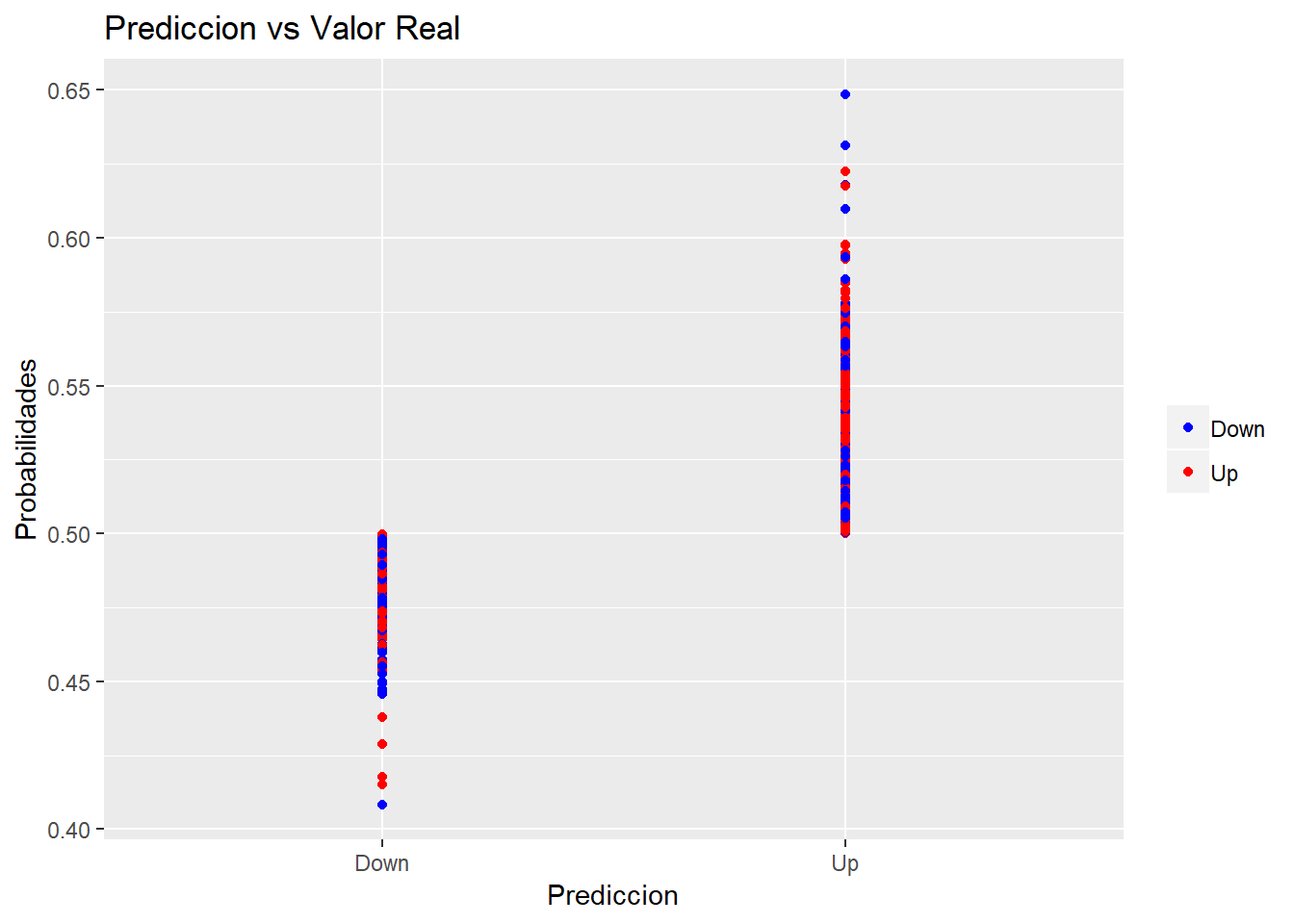
mean(glm.pred != Smarket$Direction)## [1] 0.4784Podemos ver de manera gráfica como han sido clasificados por nuestro modelo (en función de la probabilidad obtenida) frente a su valor real.
nuevo <- data.frame(glm.probs, glm.pred, Smarket$Direction)
names(nuevo)[1] <- "probs"
names(nuevo)[2] <- "pred"
names(nuevo)[3] <- "direction"
nuevo$direction <- ifelse(nuevo$direction == 1, 'Up', 'Down')
nuevo$pred <- ifelse(nuevo$pred == 1, 'Up', 'Down')
library(ggplot2)
ggplot(data = nuevo,
aes(x = pred, y = probs, col = direction)) + geom_point() +
labs(x = 'Prediccion', y = 'Probabilidades') +
ggtitle('Prediccion vs Valor Real') +
theme(legend.title=element_blank()) +
scale_colour_manual(values=c("blue", "red"))