6.2 Modelo Logit
El objetivo de los modelos de regresión logística es encontrar el mejor ajuste para describir las relaciones entre las variables respuesta (dicotómica o cualitativa) y un grupo de variables explicativas. Esta diferencia (respecto a los modelos con variable respuesta cuantitativa) da lugar a distintos modelos paramétricos y a distintas hipótesis para estos modelos, pero, una vez salvada esta diferencia, los métodos empleados en Regresión Logística siguen los principios generales de los métodos de Regresión Lineal.
La primera razón por la cual un Modelo de Regresión Lineal no es adecuado para este tipo de datos es que la variable respuesta sólo puede tomar 2 valores (0 y 1), de modo que si pretendiésemos elaborar una relación entre una variable explicativa y esta, tendríamos que condicionar la probabilidad de alguno de los valores de la variable respuesta a cada valor de la variable explicativa, es decir \(E(Y= 1 | X = x_1)\) y obtendríamos la curva logística:
La relación existente no es lineal, sino que puede asociarse con la función de distribución de cierta variable aleatoria. Al utilizar la distribución Logística, representaremos la media de \(Y\), dado un valor \(x\) de la variable \(X\), por \(\pi(X)=E(Y/x)\).
El modelo de Regresión Logística es: \[ \pi(x) = \frac{e^{\beta_0+\beta_1x}}{1+e^{\beta_0+\beta_1x}} \] o de forma equivalente: \[ \pi(x) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x)}} \]
Aplicando la transformación Logit: \[ g(x)=\ln\Big[\frac{\pi(x)}{1-\pi(x)}\Big]= \beta_0+\beta_1x \]
Hemos llegado a \(g(x)\), que tiene las propiedades que se desea que tenga un Modelo de Regresión Lineal; es lineal en sus parámetros; puede ser continua y su rango está entre \(-\infty\) y \(\infty\) dependiendo del rango de X.
Como hemos dicho antes, también tenemos que tener clara la distribución de la parte aleatoria de nuestro modelo. En el Modelo Lineal Generalizado suponemos que un valor de la variable dependiente puede expresarse como \(y=E(Y/x)+\epsilon.\) Donde \(\epsilon\sim N(0,\sigma^2)\), con varianza constante para los distintos niveles de la variable independiente. Pero esto no ocurre así en el caso de una variable dicotómica.
Si expresamos nuestro modelo como \(Y = \pi(x) + \epsilon,\) \(\epsilon\) toma dos posibles valores:
- Si \(Y=1,\) con probabilidad \(\pi(x)\), \(\epsilon= 1-\pi(x)\), con probabilidad \(\pi(x)\).
- Si \(Y=0, \epsilon = -\pi(x)\), con probabilidad \(1-\pi(x)\).
Por tanto: \[ E(\epsilon)= (1-\pi(x))\pi(x)-\pi(x)(1-\pi(x))=0 \]
\[ V(\epsilon) = (1-\pi(x))^2\pi(x)-\pi(x))^2(1-\pi(x))=\pi(x)(1-\pi(x)) \]
La distribución de la variable dependiente \(Y\), dado un valor de \(x\) de la variable \(X\), sigue una distribución Binomial con probabilidad \(\pi(x)\).
Al no ser una relación lineal, no es posible interpretar directamente el valor de los parámetros estimados. Para ello se utilizan los ‘ODDS Ratios’.
A través de un ratio de ODDS se puede calcular qué influencia genera en el target el incremento de una unidad en el valor de la variable explicativa.
- Si \(\beta_i > 0\) el efecto de la variable explicativa \(X_i\) sobre la respuesta \(Y\) es de incremento: aumenta la probabilidad del target.
- Si \(\beta_i < 0\) el efecto que produce la variable explicativa \(X_i\) sobre la respuesta \(Y\) es decremento: disminuye la probabilidad del target.
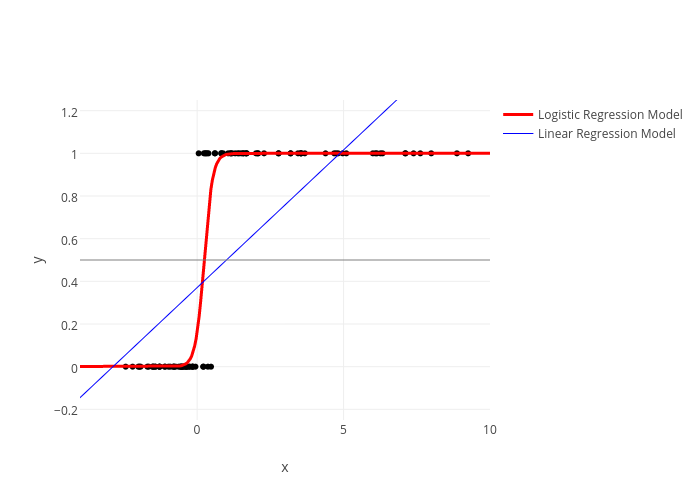
Cuando la variable respuesta es continua, se utilizan métodos de regresión lineal o de otro tipo; en cambio, cuando la variable respuesta es cualitativa se utilizan los llamados Modelos de Regresión Logística.