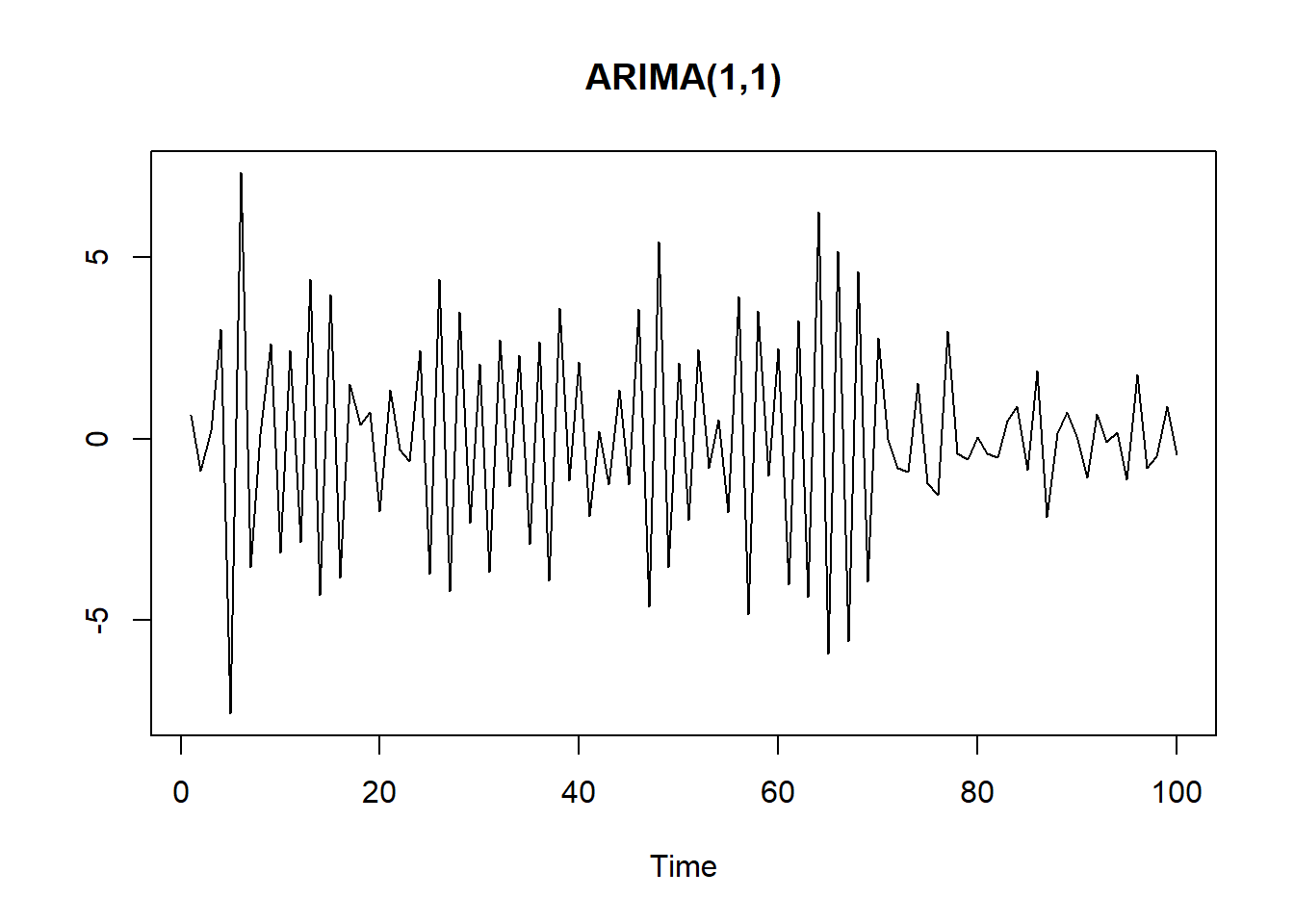
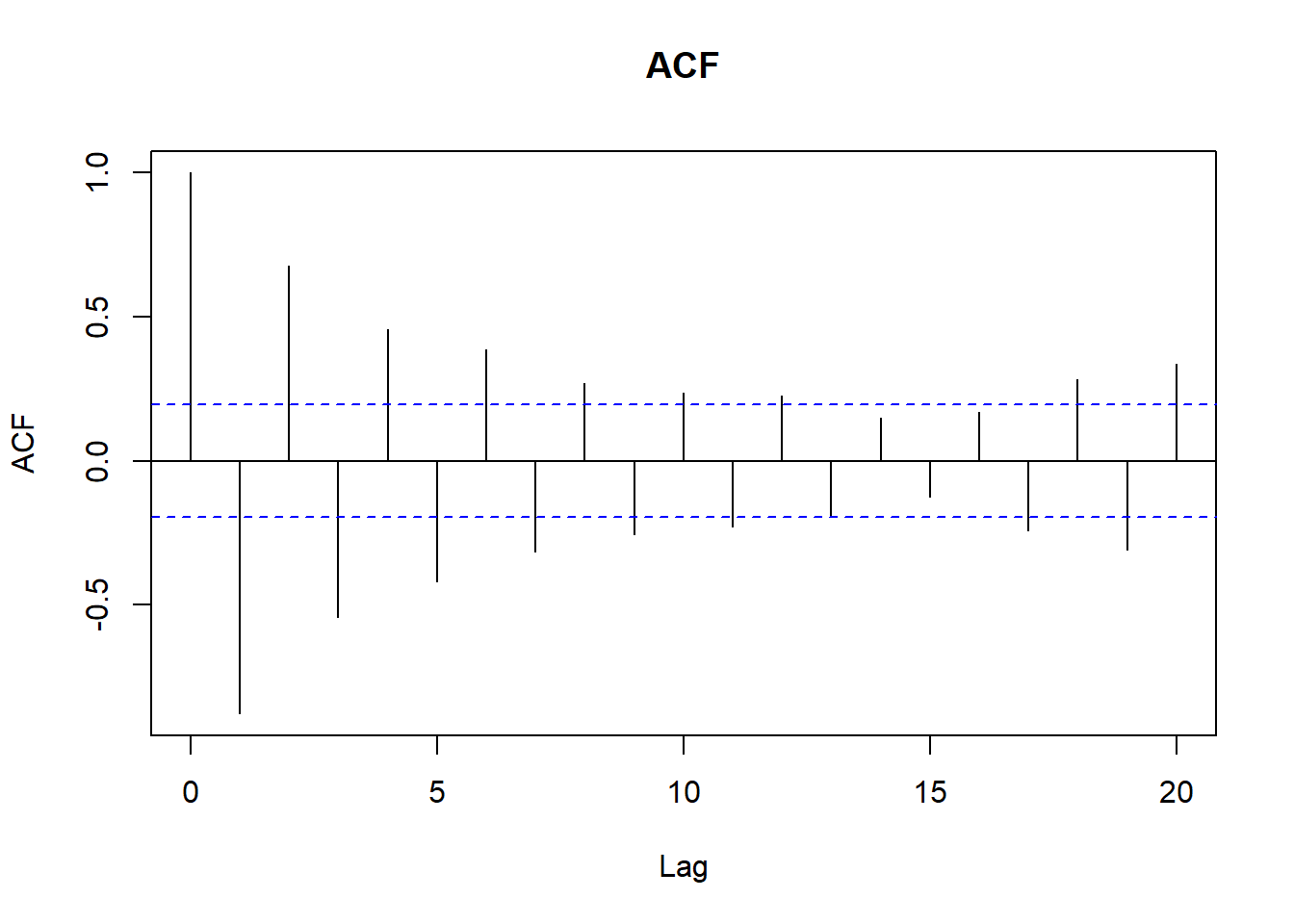
7.4 ARIMA
Un proceso estocástico es un mecanismo generador de un número aleatorio de series. Una serie temporal es una realización particular de un proceso estocástico.
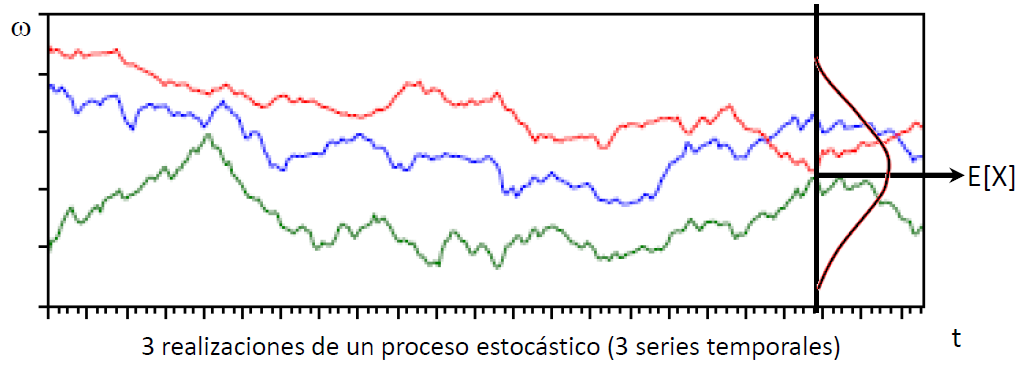
El objetivo que se plantea es inferir el proceso estocástico que ha generado el conjunto de observaciones que definen la serie temporal.
Para caracterizar un proceso estocástico \(F(y(t_1),\ldots,y(t_N))\), se requiere de la distribución conjunta de \(F(y_t), \forall t\), las distribuciones marginales \(F(y_t,y_{t+1}), \forall t\), etc.
Problema. Como sólo se dispone de una observación por instante temporal, no es posible obtener dichas distribuciones.
Solución. Asumir qe las distribuiones son estables (estacionarias) en el tiempo para que las distribuciones asociadas a diferentes instantes sean comparables.
Un proceso es estacionario en sentido estricto si el comportamiento de una colección de variables aleatórias sólo depende de su posición relativa, no del instante \(t\).
Una vez que el proceso (serie) es estacionario, se busca algún tipo de modelo adecuado para su caracterización: los procesos ARMA son modelizables mediante modelos ARMA.
\[ARMA(p,q) = (1-\phi_1 B - \ldots - \phi_p B^p)X_t = (1- \theta_1 B - \ldots - \theta_q B^q)a_t\]
7.4.1 Parte AR (Autorregresiva)
La parte autogresica del modelos muestra la dependencia del dato real con su propio pasado. Se trata de una regresión de la variable en sí misma (autoregresión).
\[AR(p): X_t= \mu_t + \phi_1X_{t-1} + \ldots + \phi_1X_{t-p} + a_t\]
7.4.2 Parte MA (Medias Móviles)
La parte de medias moviles muestra la dependencia del dato real con el pasado del proceso de error (media móvil de la serie de los errores)
Los procesos \(MA\) siempre son estacionarios.
\[MA(q): X_t= \mu - \theta_1 a_{t-1} - \ldots - \theta_q a_{t-q} + a_t\]
Se requiere identificar el proceso que buyace bajo los datos, lo cual consiste en identicar los órdenes \(p\) y \(q\) del modelo ARMA que generó la serie temporal.
Las herramientas para identificar esos procesos son las funciones de autocorrelación simple y parcial.
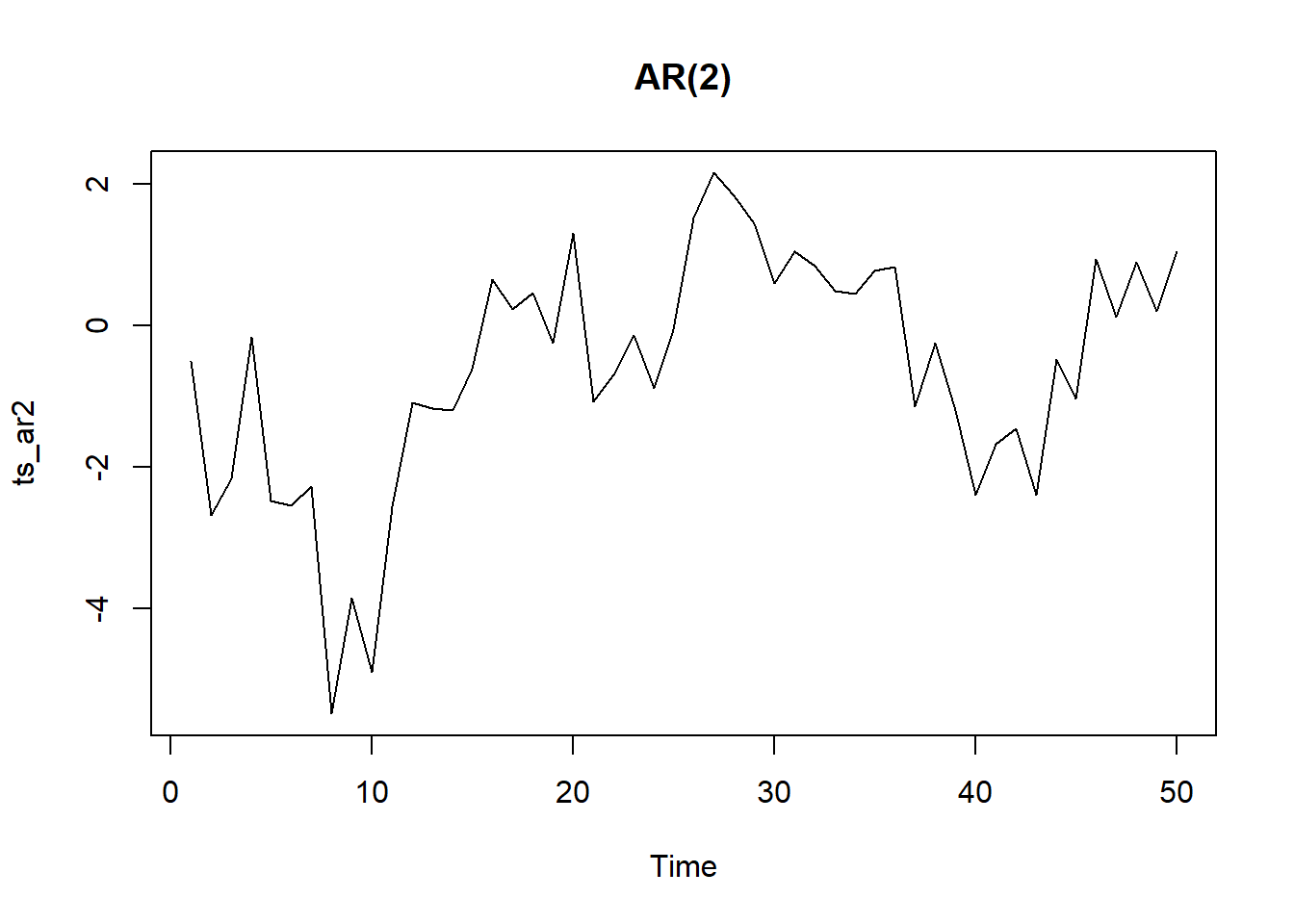
Ejemplo AR(2): \(Y_t = 0.6Y_{t-1}+0.2Y_{t-2}+A_t\)
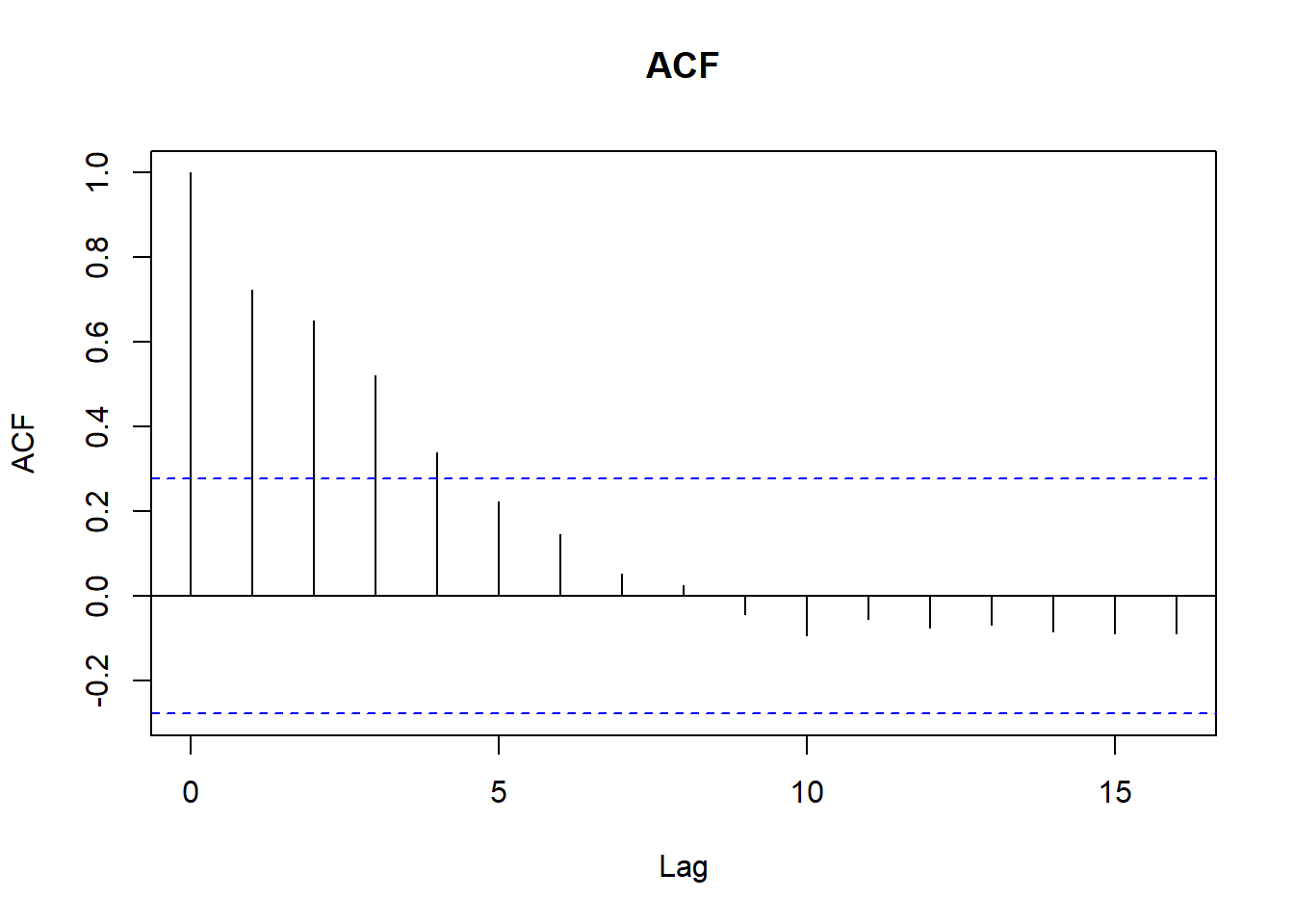
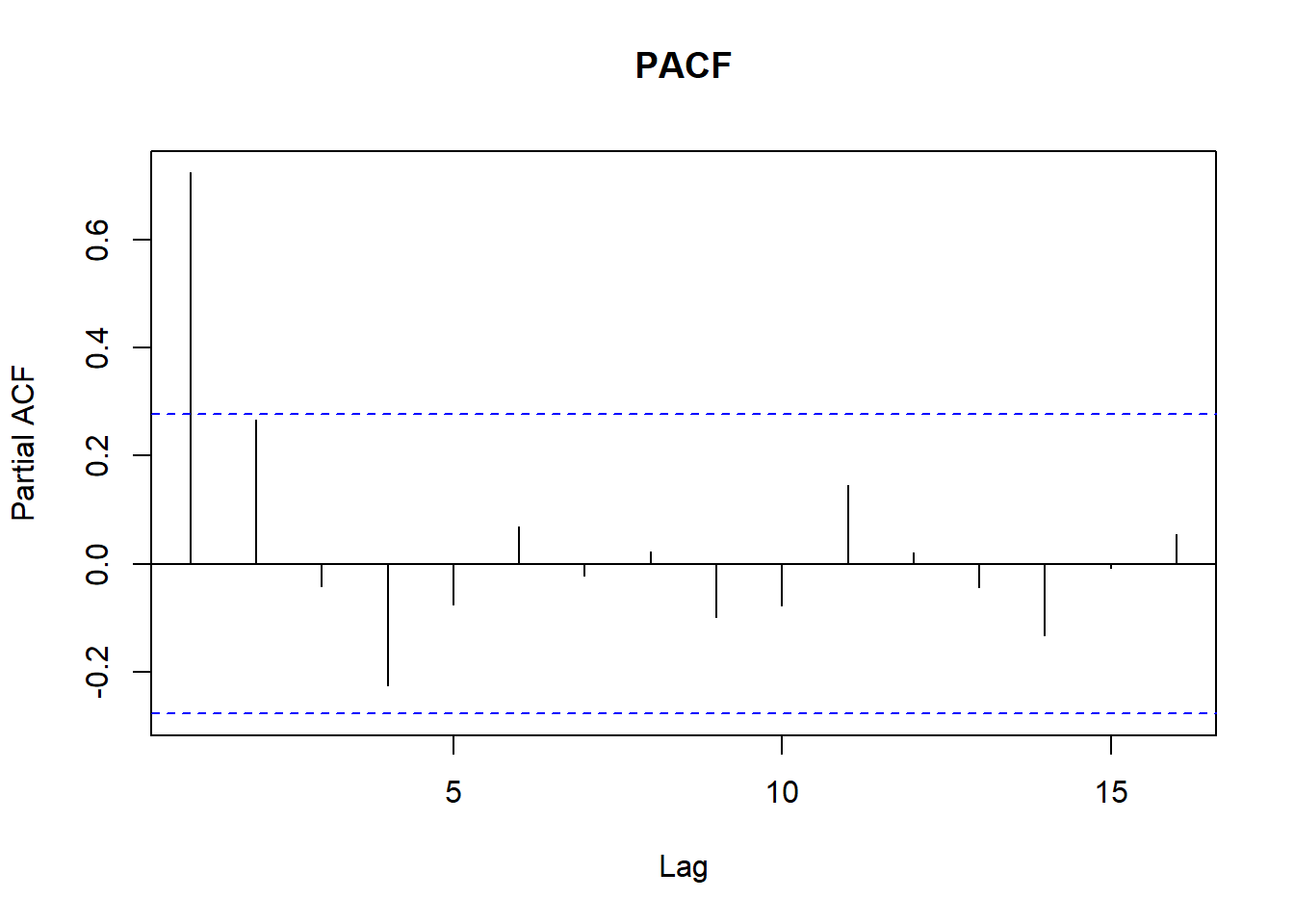
Ejemplo MA(2): \(X_t=A_t-0.6A_{t-1}-0.2A_{t-2}\)
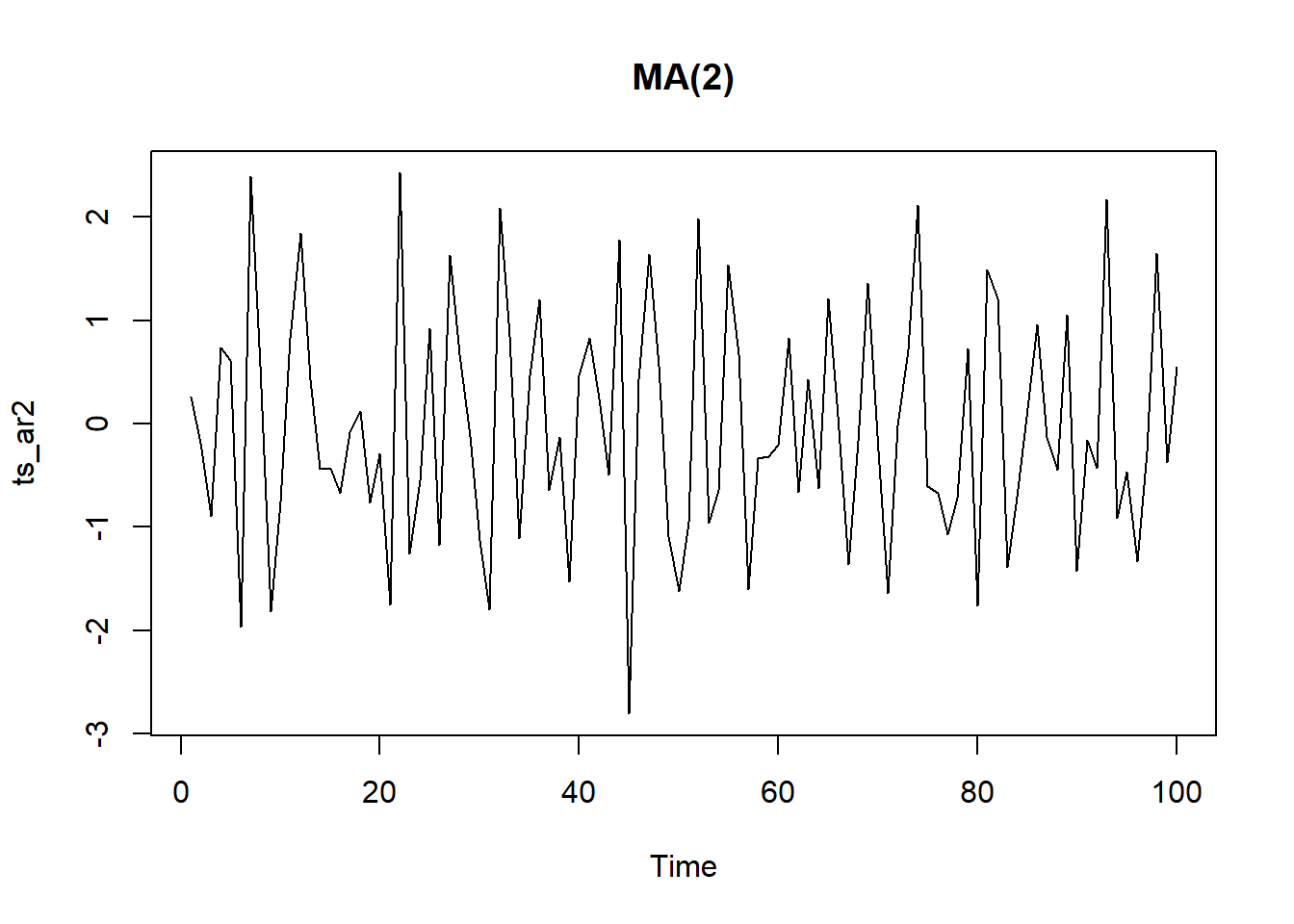
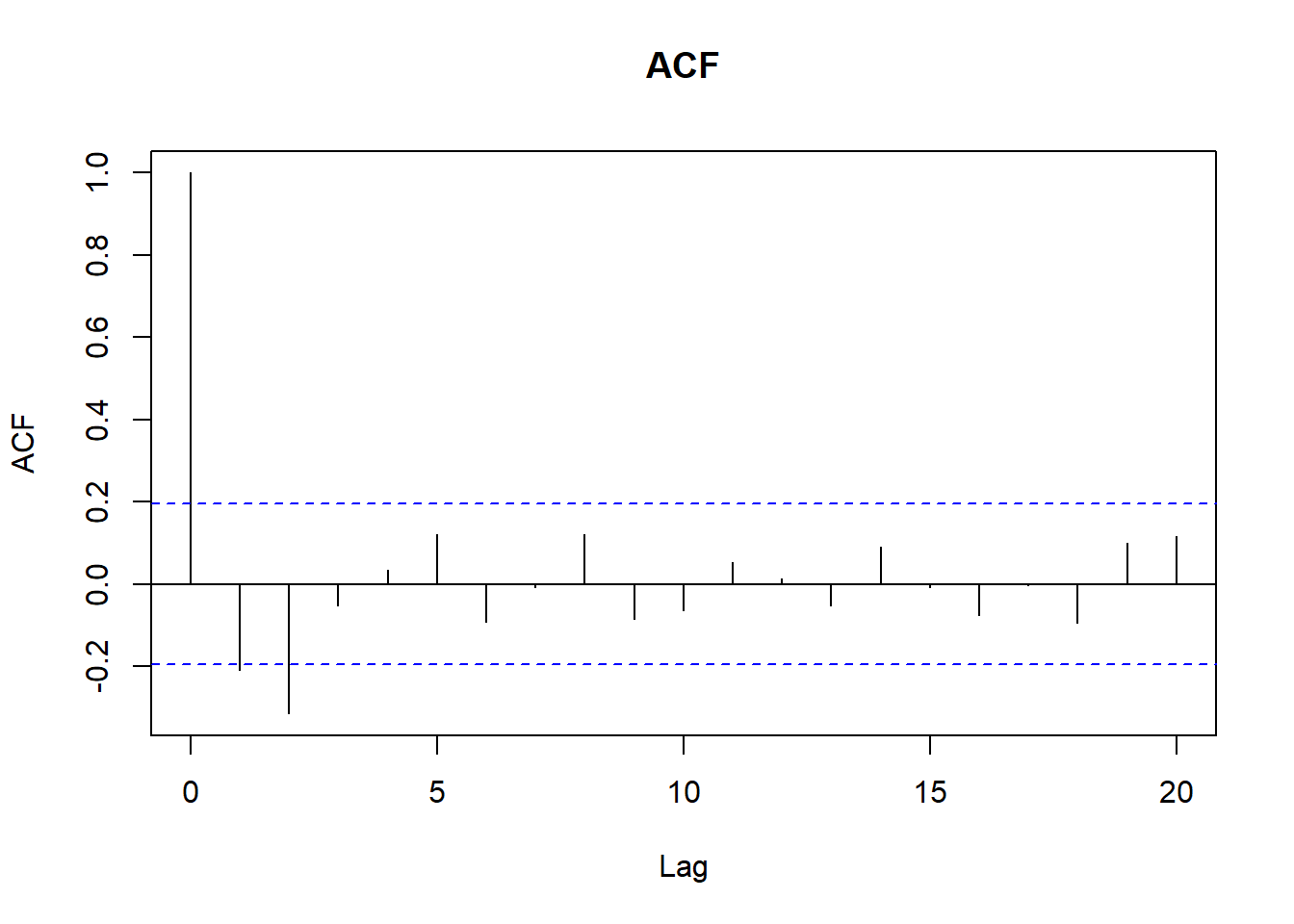
Ejemplo ARIMA(1,1):\(Y_t = -0.8 Y_{t-1} + A_t -0.8A_{t-1}\)