9.2 Hierarchical clustering
9.2.1 Modelo
El agrupamiento jerárquico es un método de análisis de grupos, el cual busca construir una jerarquía de grupos. Hoy dos tipos de estrategias para agrupamiento jerárquico:
Aglomerativas: Este es un acercamiento ascendente. Cada observación comienza en su propio grupo y los pares de grupos son mezclados mientras uno sube en la jerarquía.
Divisivas: Este es un acercamiento descendente. Todas las observaciones comienzan en un grupo y se realizan divisiones mientras uno baja en la jerarquía.
Es aconsejable usar los métodos aglomerativos, ya que tienen menor orden de complejidad. Por esta razón nos centraremos en los métodos aglomerativos.
El algoritmo funciona de la siguiente manera:
- Colocar cada punto en su propio clúster.
- Identificar los dos clústers más cercanos y combinarlos en un clúster.
- Repetir el paso anterior hasta que todos los puntos estén en un solo clúster.
Hay varios criterios de enlace:
- Agrupamiento de máximo o completo enlace.
- Agrupamiento de mínimo o simple enlace.
- Agrupamiento de enlace media o promedio (UPGMA).
- Agrupamiento de mínima energía.
- La suma de todas las varianzas intra-grupo.
- El decrecimiento en la varianza para los grupos que están siendo mezclados (criterio de Ward).
- La probabilidad de que grupos candidatos se produzcan desde la misma función de distribución (V-enlace).
9.2.2 Implementación en R
Como en la sección anterior usaremos el data set de iris, así podremos comparar los métodos.
Los árboles jerárquicos se suelen representar con un dendograma.
set.seed(44)
hclusters = hclust(dist(iris[, 3:4]), method = "complete")
plot(hclusters)
abline(h = 3, col = "red")
abline(h = 2, col = "red")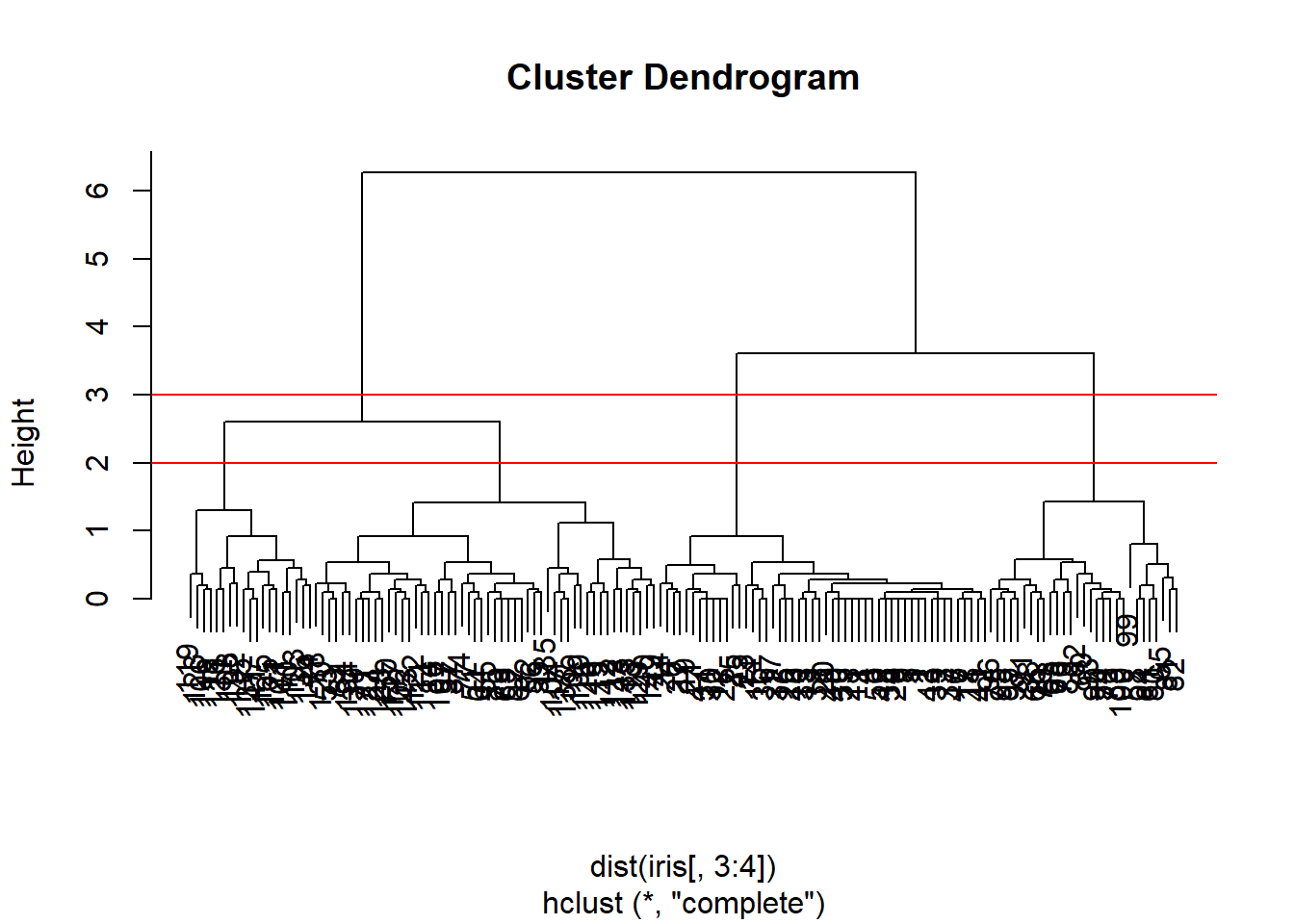
Como podemos observar en el dendograma el número óptimo de clusters es tres o cuatro. Seleccionamos tres para comparar con Species.
clusterCut = cutree(hclusters, 3)
table(clusterCut, iris$Species)##
## clusterCut setosa versicolor virginica
## 1 50 0 0
## 2 0 21 50
## 3 0 29 0p = ggplot() + geom_point(data = iris, aes(x = Petal.Length, y = Petal.Width, shape = iris$Species, color = as.factor(clusterCut)))
p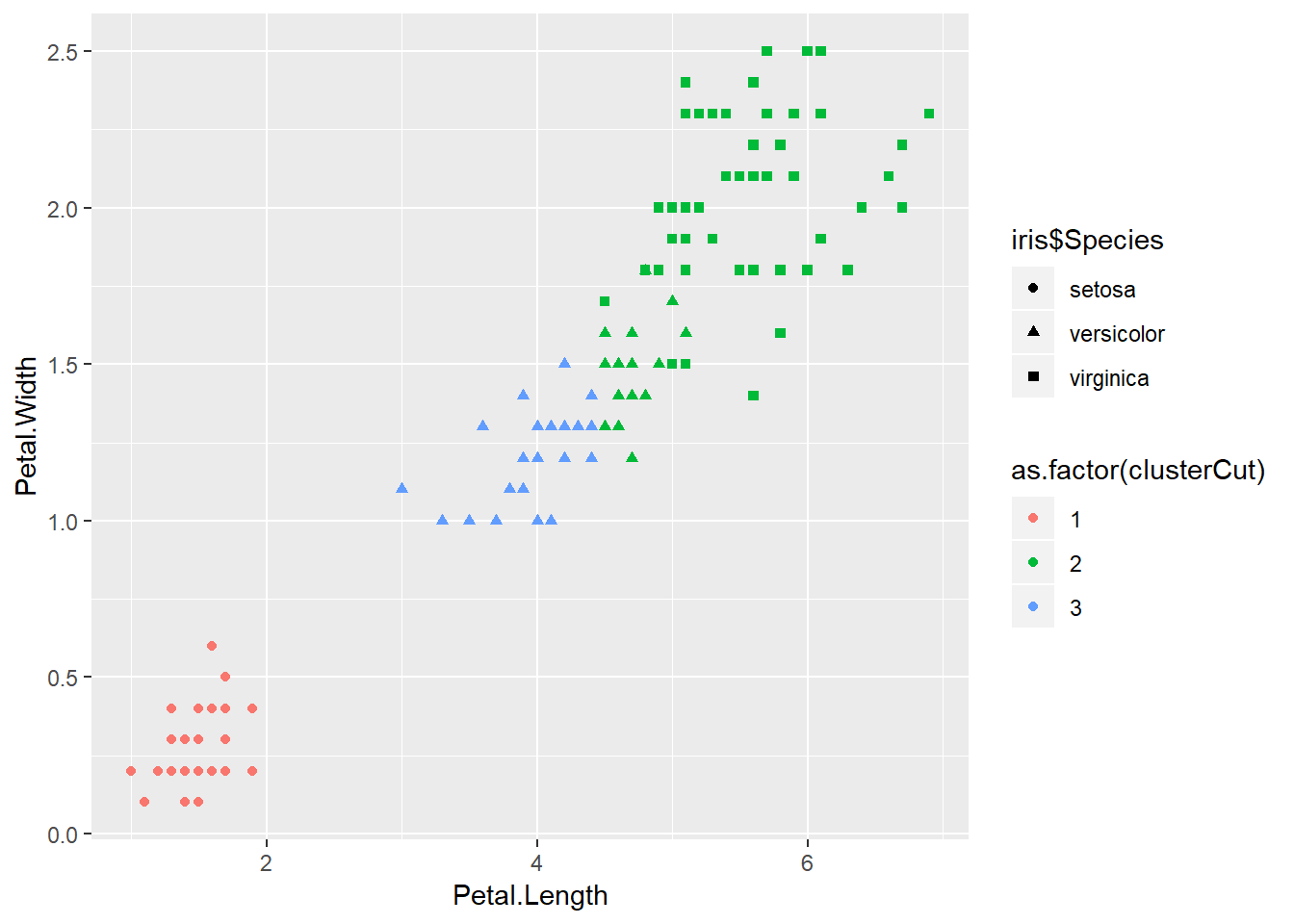
Parece que este método no va muy bien. Probamos ahora usando el criterio de agrupamiento de enlace media o promedio (UPGMA).
hclusters <- hclust(dist(iris[, 3:4]), method = 'average')
plot(hclusters)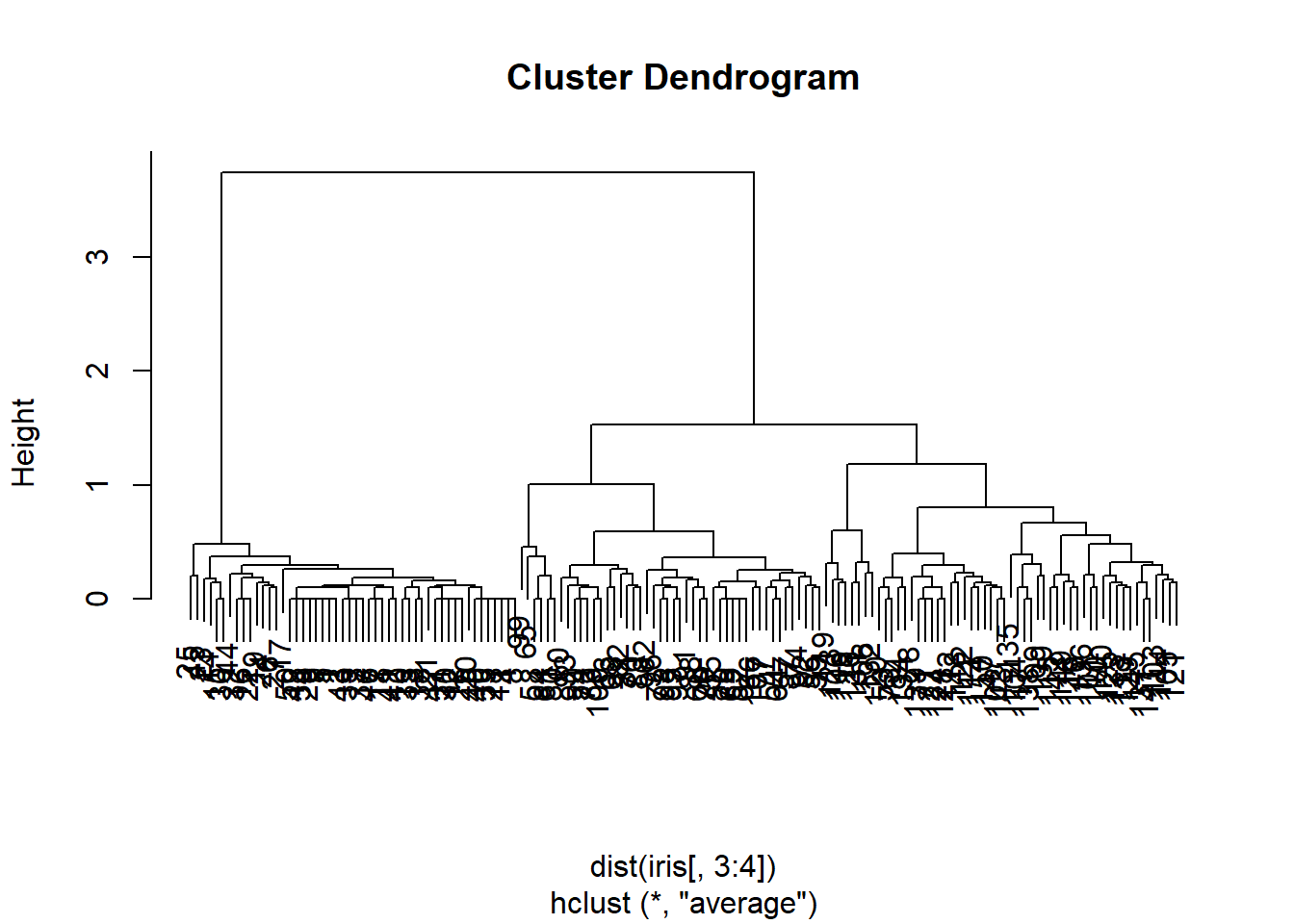
clusterCut = cutree(hclusters, 3)
table(clusterCut, iris$Species)##
## clusterCut setosa versicolor virginica
## 1 50 0 0
## 2 0 45 1
## 3 0 5 49p = ggplot() + geom_point(data = iris, aes(x = Petal.Length, y = Petal.Width, shape = iris$Species, color = as.factor(clusterCut)))
p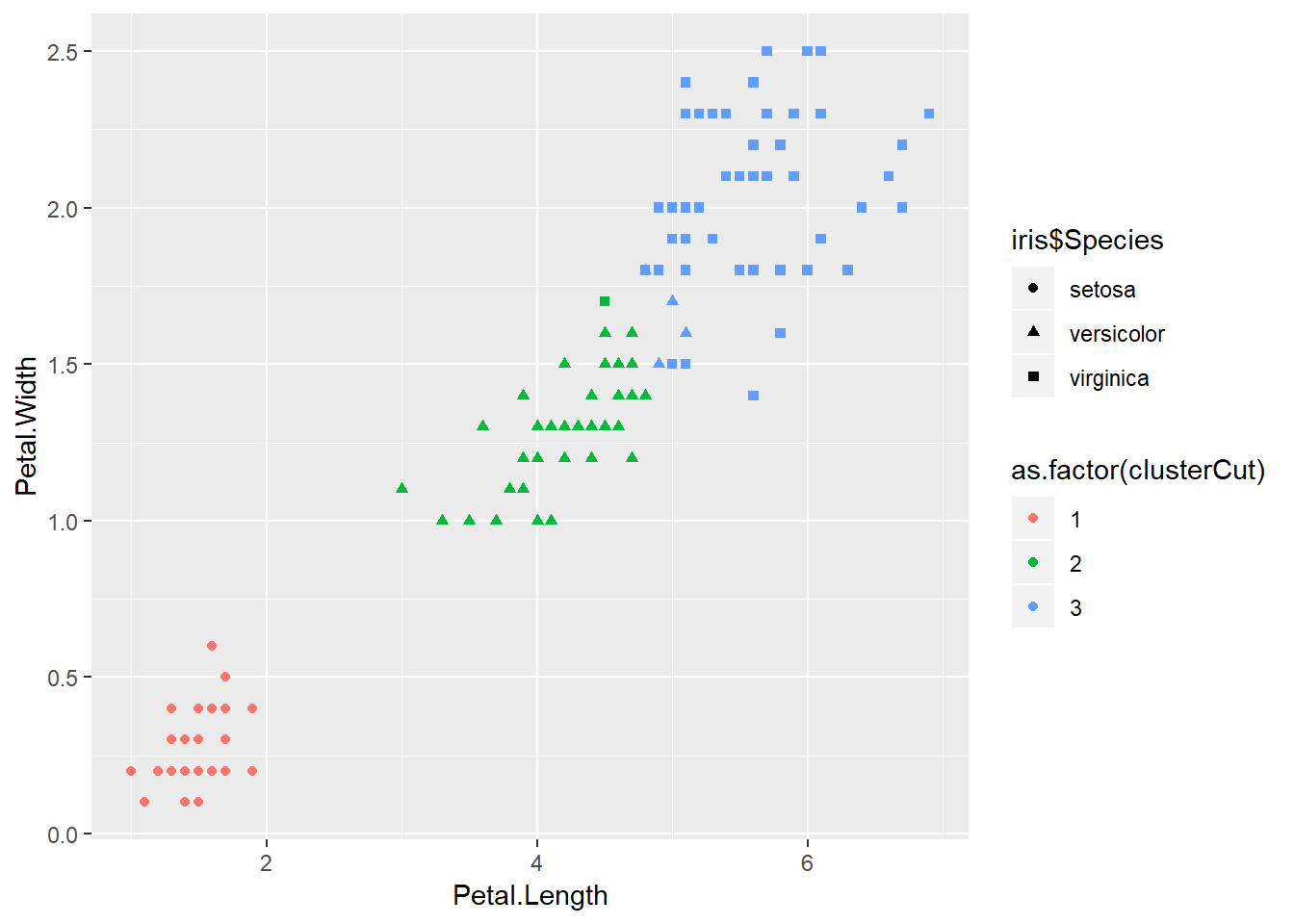
Estos resultados ya nos gustan más. Hay que recordar que normalment no podemos calcular la matriz de confusión en el aprendizaje no supervisado.
La evaluación es análoga al método de K-means. La evaluación de los métodos no supervisados suele ser algo un poco subjetivo. Hay que buscar una métrica que se ajuste al problema y comparar distintos métodos y parámetros.