10.2 Bagging y Random Forest

Uno de los problemas de los árboles de decisión es su alta varianza, es decir, un ligero cambio en los datos puede producir un gran cambio en la estructura del árbol. Para paliar este hecho, los modelos de bagging actúan de la siguiente forma:

• Se obtienen \(n\) muestras bootstrap.
• Se ajusta un modelo para cada una de las muestras.
• La predicción final será la media de las predicciones.

Las muestras bootstrap consisten en seleccionar con reemplazamiento muestras de las observaciones originales.

Esta idea se puede aplicar desde otro enfoque. Pueden existir variables que sean muy buenas predictoras y, aunque escojamos muestras bootstrap, puede que lso árboles siempre escojan estas variables haciendo que otras varaibles menos buenas no sean tenidas nunca en cuenta. Para ello, el modelo random forest actúa de la misma forma que el método de bagging pero **muestreando sobre las columnas en vez de las observaciones. Esto favorece que puedan intervenir variables que, a priori, no son tan buenas predictoras.

10.2.1 En R

FALSE 
FALSE Call:
FALSE  randomForest(formula = medv ~ ., data = Boston, mtry = 13, importance = TRUE,      subset = train) 
FALSE                Type of random forest: regression
FALSE                      Number of trees: 500
FALSE No. of variables tried at each split: 13
FALSE 
FALSE           Mean of squared residuals: 10.80817
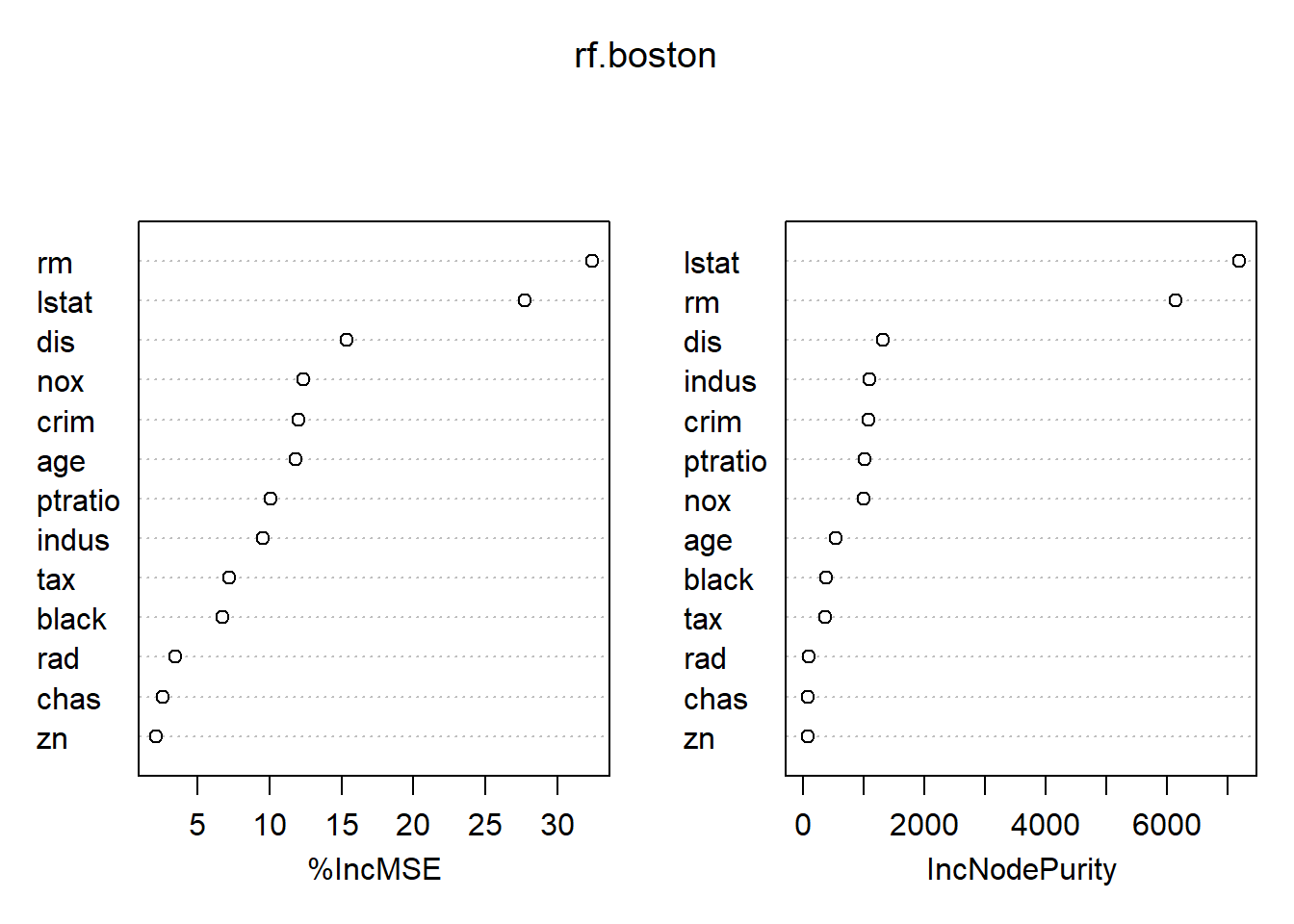
FALSE                     % Var explained: 86.91

FALSE           %IncMSE IncNodePurity
FALSE crim    12.042248    1083.56152
FALSE zn       2.144551      76.90258
FALSE indus    9.518353    1088.06694
FALSE chas     2.591068      77.14216
FALSE nox     12.346546    1002.78940
FALSE rm      32.409454    6134.55720
FALSE age     11.799314     530.13915
FALSE dis     15.362428    1309.52619
FALSE rad      3.468537      96.05578
FALSE tax      7.196484     361.87594
FALSE ptratio 10.103258    1018.55792
FALSE black    6.737108     384.53170
FALSE lstat   27.720132    7184.83340